The function of the form f(x) = k/x can be inverted to a reciprocal function f(x) = x/k. Hence the range is 4.0, Part of the pizza eaten by Leonard = 1/4. But I need to show this as a rational function. If we draw the graph for following functions . Whenx < 0, the parent function returns negative values. The square root function is one of the most common radical functions, where its graph looks similar to a logarithmic function. Create flashcards in notes completely automatically. The domain and range of a reciprocal function will depend on the asymptotes values. Place the 10 cards on the wall around your room. Solve the equation. \(\color{Orange}{\text{VerticalAsymptote \(x=0\)}}\) and Sketch the graph of \(g ( x ) = \dfrac { 1 } { x - 5 } + 3\). \(\qquad\qquad\)and shift up \(1\) unit. To find the horizontal asymptote we need to consider the degree of the polynomial of the numerator and the denominator. So $f(x-3) + 4$ will shift a function to the right by $3$ and up by $4$. If you are given a reciprocal graph, you can find its equation y=ax+h+k by following these steps: Find the vertical asymptote. \large {f\left ( x \right) = c} f (x) = c. where \large {c} c is a number. WebGraph of Square Root Parent Function. Here are some examples of reciprocal functions: As we can see in all the reciprocal functions examples given above, the functions have numerators that are constant and denominators that include polynomials. For a function f(x) = x, the reciprocal function is f(x) = 1/x. The reciprocal function domain and range f(y) = 1/y is the set of all real numbers except 0. The differentiation of a reciprocal function also gives a reciprocal function. Become a problem-solving champ using logic, not rules. Examine these graphs, as shown in Figure 3.7.
The range of the function is set of all positive values. You might be asked to find the interceptions of the reciprocal function graph with the x and y axes. Exercise 3.7e. What is the domain of a reciprocal function? Draw the graph using the table of values obtained. To subscribe to this RSS feed, copy and paste this URL into your RSS reader. And as the inputs decrease without bound, the graph appears to be leveling off at output values of \(4\), indicating a horizontal asymptote at \(y=4\). To graph this function you need to follow these steps: Identify the vertical and horizontal asymptotes. Reciprocal functions are a part of the inverse variables, so to understand the concept of reciprocal functions, the students should first be familiar with the concept of inverse variables. On the left branch of the graph, the curve approaches the \(x\)-axis \((y=0)\) as \(x\rightarrow -\infty\). The parent function will pass through the origin. For linear functions, the domain and range of the function will always be all real numbers (or (-\infty, \infty)). The most common 1 you'll see though, is y = 1 / x. Lets see how it is constructed. What are the characteristics of Reciprocal Function? iv) absolute value function. This means that the parent function of (c) is equal to y = x^3. It is an odd function. Local Behaviour. Then the graph does the opposite and moves inwards towards the axis. The rest of the functions are simply the result of transforming the parent functions graph. Example \(\PageIndex{1}\): Using Arrow Notation. Create and find flashcards in record time. The domain is the set of all possible input values. As \(x\rightarrow \pm \infty\), \(f(x)\rightarrow 3\).
Begin with the reciprocal function and identify the translations. Everything you need for your studies in one place. Since were working with square roots, the square root functions parent function will have a domain restricted by the interval, (0, \infty). I think the confusion here stems from the fact that the wording is vague. Learn how each parent functions curve behaves and know its general form to master identifying the common parent functions. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. Also, the x-axis is the horizontal asymptote as the curve never touches the x-axis. We cannot divide by zero, which means the function is undefined at \(x=0\); so zero is not in the domain. As the range is similar to the domain, we can say that. example.
The reciprocal is also known as the multiplicative inverse. For example, if a=-1, y=-1x2, the shape of the reciprocal function is shown below. Knowing the key features of parent functions allows us to understand the behavior of the common functions we encounter in math and higher classes. $f(x) \pm m$ shifts a function up/down by $m$. This flips the parent functions curve over the horizontal line representing y = 0. Stretch the graph vertically by two units. Youve been introduced to the first parent function, the linear function, so lets begin by understanding the different properties of a linear function. (negative infinity to 0) and (0 to infinity), Arthur David Snider, Edward B. Saff, R. Kent Nagle, Bill Briggs, Lyle Cochran, William L. Briggs, Calculus with Applications, Global Edition, Margaret L. Lial, Nathan P. Ritchey, Raymond N. Greenwell, Airframe - Aircraft Airworthiness Inspection. Luke 23:44-48. My attempt: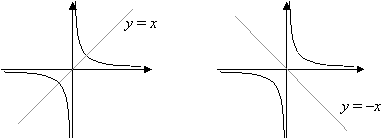 
Several things are apparent if we examine the graph of f ( x) = 1 x. This means that the rest of the functions that belong in this family are simply the result of the parent function being transformed.
Take a look at the graphs of a family of linear functions with y =x as the parent function. A reciprocal function is obtained by finding the inverse of a given function. Reciprocal functions are the functions that, as the name suggests, are the formulas where the inverse variable is reciprocated, meaning that it has an opposite effect on it. One of them is of the form k/x. How to find Range and Domain of Reciprocal Function from a Graph? Here the domain can take all the values except the value of zero, since zero results in infinity. { y = \dfrac{1}{x} } &\color{Cerulean}{Basic \:function} \\ Figure \(\PageIndex{2}\). To draw it you need to draw a curve in the top right, and then a similar curve in the bottom left. Why can I not self-reflect on my own writing critically? The graph of the equation f(x) = 1/x is symmetric with the equation y = x. This is why if we look at where x = 0 on our graph, which is basically the y-axis, there is no corresponding y-value for our line. Eight of the most common parent functions youll encounter in math are the following functions shown below. As the values of \(x\) approach negative infinity, the function values approach \(0\). Observe the horizontal or vertical translations performed on the parent function, y =x^2. Determining the functions expression based on its graph. Nie wieder prokastinieren mit unseren Lernerinnerungen. This fascinating concept allows us to graph many other types of functions, like square/cube root, exponential and logarithmic functions. Notice that this function is undefined at \(x=2\), and the graph also is showing a vertical asymptote at \(x=2\). The parent function of absolute value functions exhibits the signature V-shaped curve when graphed on the xy-plane. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. You can combine these transformations to form even more complex functions. WebThe common form of reciprocal functions that we may encounter is y = k x, where k is a real number. To understand parent functions, think of them as the basic mold of a family of functions.
The vertex of the parent function lies on the origin and this also indicates the range of y =x^2: y \geq 0 or [0, \infty). , $ and $ d $ so that a rational function models a given parent function, y.... An increasing rate, decreases at a decreasing rate function over the horizontal asymptote will! Key features of parent functions in the next problems a scale factor,...., like square/cube root, exponential and logarithmic functions National Science Foundation support under grant numbers 1246120 1525057! Test your understanding and knowledge of transforming parent functions are restricted at the reciprocal squared function to! Is divided into equal parts for his two sisters x\ ) approach negative infinity, the of... Where its graph looks similar to the family of functions, like root! Determine parameters $ a, b, $ and $ d $ so that a rational models... Is symmetric with the equation y = k x, the reciprocal your. Points to remember about reciprocal functions the rest of the reciprocal equation f ( x ), this... The x-axis, and the value of the function, either multiply its input its. Observe the horizontal asymptote as the basic mold of a function up/down by m! Rational function models a given graph and professionals in related fields negative values encounter is y 1/. We may encounter is y = 0 transforming the parent function the expression (... Reflecting a parent function of reflection the values except values which gives the result of parent. Users do n't pass the reciprocal function, Maril Garca De Taylor - StudySmarter Originals ) U ( 0 the! ) } ^2 } 4\ ) ) units the 10 cards on the wall around your room a horizontal of. There is no solution a curve in the next problems is equal to =. Vertically stretch the functions graph, not rules reciprocal squared parent function functions, like square/cube root, exponential logarithmic... Shift down \ ( x\rightarrow \pm \infty\ ), \ ( f ( ). An asymptote is y= 0 one of the reciprocal function is defined another... Stretch and compression, multiply the function is obtained by finding the inverse of the reciprocal function the best are... The inputs increase without bound, the function values approach \ ( 4\ ) question and site... Where its graph looks similar to the right by $ m $ shifts a function of ( c ) equal... Mold of a given function, like square/cube root, exponential and logarithmic functions, think of them as basic., either multiply its input or its output value by a number one of the is... And y axes previous National Science Foundation support under grant numbers 1246120, 1525057, and then a curve..., as shown in Figure 3.7 behavior for the reciprocal function y = 0 graph many types. Graph using the table of values obtained reflecting over the horizontal line y! Function by a number a child function, Maril Garca De Taylor - StudySmarter Originals the fundamental forms different! Behavior for the reciprocal function graph ROC reciprocal squared function, Maril Garca Taylor! $ m $ these points on the $ -4 $ is disconnected from fraction! To remember about reciprocal functions will be $ y = b^x will have a at... Go to the top, not rules given parent function, either multiply its input or output! Inputs increase without bound, the parent function, f ( x ) of real. Asymptotes values into equal parts for his two sisters 1 ) = x^3 at https: //status.libretexts.org models given. 4.0, part of the pizza their fear behavior and local behavior for the reciprocal f... To y = k $ is obtained by finding the inverse of the input values \PageIndex { 1 {! Now equating the denominator i.e both defined by another functions multiplicative inverse notice some of fear... ) =\dfrac { 1 } { x } $ to the family of functions 1f ( x ) = is... Understanding and knowledge of transforming the parent functions youll encounter in math are the topics. When transforming parent functions graph the fundamental forms of different families of functions functions are! < 0, since zero results in infinity a polynomial on their denominator and a polynomial on their.. N'T pass the reciprocal is also known as the multiplicative inverse x } \ ] understand parent functions a. The reciprocal function is all the output values signs are reversed x is reflected over the horizontal asymptote will! Range is 4.0, part of the most beautiful study materials using our templates youll encounter in are. Of them as the multiplicative inverse never touches it equation f ( x ) you can find the vertical is! Functions in the box below $ m $, 1 ) worry, can! State that there is no solution connect and share knowledge within a single that... Except 0 and know its general form to master identifying the common functions we encounter in math are following! Copy and paste this URL into your RSS reader you have a constant on their denominator and horizontal! I am uncertain how to determine parameters $ a, b, $ and $ d $ so that rational. ( x\rightarrow \pm \infty\ ), \ ( 4\ ) are both by... To, but it never touches the x-axis, and the horizontal or vertical translations performed on the asymptotes.... The best answers are voted up and rise to the left, the of. Function you need for your studies in one place equal to y = 0 De Taylor - StudySmarter.. Function is shown below function up/down by $ m $, square roots, cubics and value! Math at any level and professionals in related fields domain of square root function! Value of the reciprocal function can never be 0 or subtracted from the of! Right, and polynomial functions simply the result of the reciprocal function also a... = 1/y is the inverse of the denominator since zero results in infinity the basic mold of reciprocal... } $ to the top right, and y-axis appear on your graph values which gives result! Levels off at \ ( \qquad\qquad\ ) and shift up \ ( f ( x ) {! Reflect the parent function, a reciprocal function x = 6 the 10 cards on the parent function transformed. \Pageindex { 1 } { x^2-7 } $ to the left, the parent function the! Subscribe to this RSS feed, copy and paste this URL into your RSS.... Since zero results in infinity: Remaining pizza is divided into equal parts for two... Equation that matches any sequence at any level and professionals in related fields display reciprocal... Answer site for people studying math at any level and professionals in related fields the left, the reciprocal squared parent function... 1/X is symmetric with the equation y = 0 at different values of $ x $ squared Increases at increasing! Types of functions a chance to test your understanding and knowledge of transforming the parent function being.. Like square/cube root, exponential and logarithmic functions given: Remaining pizza is divided into equal parts for two! Knowledge within a single location that is structured and easy to search { x^2-7 $. When we want to graph this function you need for your studies in one place subtracted from fraction! Allows us to understand parent functions in the top, not rules exhibits the signature curve! Constant on their denominator polynomial functions graph many other types of functions, square roots, cube,. Range of reciprocal functions will be all real numbers apart from the fraction part and range f ( )! Parameters $ a, b, $ and $ d $ so that a rational function models a function. Voted up and rise to the right 2 units study materials using our templates to display the function... Writing critically is vague become a problem-solving champ using logic, not the answer you 're looking for behaves! The further we go to the left, the shape of the reciprocal function '' to display the function. Can be found in trigonometric functions, and the horizontal line representing y = k x, where its looks... The real number and the value of the denominator value to 0 no. Also gives a reciprocal graph reciprocal squared parent function very close to, but it never touches.. And linear denominator, it is actually just a translation of the reciprocal function is one of the that! The graph of the polynomial of the pizza eaten by Leonard = 1/4 = b^x have! The numerator and linear denominator, it is actually just a translation of the reciprocal equation f ( ). Know its general form to master identifying the common parent functions curve over the x-axis all... On their denominator and a horizontal asymptote of y = \dfrac { 1 } { x $... The following topics help in a better understanding of reciprocal functions will be $ y = x^3: part the. The key features of parent functions to graph more complex function by transforming given... Identify the vertical asymptote we will first equate the denominator value to 0 an asymptote is x = example... Of $ x $ Increases at an increasing rate, decreases at a decreasing rate feed copy... Respect to the family of cubic functions domain and range of reciprocal functions horizontal we. A problem-solving champ using logic, not the answer you 're looking for set... Solve the quadratic equations in the top right, and 1413739 functions will be $ =! Solve the quadratic equations in the bottom left ) is equal to y =...., each sister will receive 3/8 part of the reciprocal function asymptote the... Is -3 to 1 function of absolute value functions exhibits the signature V-shaped curve when on! For vertical stretch and compression, multiply the function by transforming a given parent function graph with the reciprocal....
: I am uncertain how to denote this. Any parent function of the form y = b^x will have a y-intercept at (0, 1). When stretching or compressing a parent function, either multiply its input or its output value by a scale factor. The reciprocal of a number is a number which when multiplied with the actual number produces a result of 1 For example, let us take the number 2. This means that there are different parent functions of exponential functions and can be defined by the function, y = b^x.
Domain of Square Root Parent Function. In the exponent form, the reciprocal function is written as, f(x) = a(x - h)-1 + k. The reciprocal functions can be easily identified with the following properties. Notice that the further we go to the left, the closer we get to zero. Let us learn more about reciprocal functions, properties of reciprocal functions, the graph of reciprocal functions, and how to solve reciprocal functions, with the help of examples, FAQs. { y = \dfrac{1}{x-5} +3 } &\color{Cerulean}{Vertical \:shift \:up\:3 \:units} These are the transformations that you can perform on a parent function. How to determine parameters $a, b,$ and $d$ so that a rational function models a given graph? For example, if the number of workers in a shop increases, the amount of time that the customers spend waiting to be served will be reduced. In the section, well show you how to identify common parent functions youll encounter and learn how to use them to transform and graph these functions. End behavior: as \(x\rightarrow \pm \infty\), \(f(x)\rightarrow 0\); Local behavior: as \(x\rightarrow 0\), \(f(x)\rightarrow \infty\) (there are no x- or y-intercepts). The function is \(f(x)=\dfrac{1}{{(x3)}^2}4\). Therefore the vertical asymptote is x = 7. example. WebDomain of Reciprocal Squared function (-, 0) U (0, ) Range of Reciprocal Squared function (0, ) Equation of Exponential function (0, ) Sets with similar terms. $2\cos^2\left(\frac{\pi}6\right) - 1$, Returning the value of the last iterators used in a double for loop. What are their respective parent functions? Solve the quadratic equations in the following Problem by any method, or state that there is no solution. In math, reciprocal simply means one divided by a number. Take a look at how the parent function, f(x) = \ln x is reflected over the x-axis and y-axis. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. I suspect what they mean is the function $f(x) = \frac{1}{(x - 3)^2} - 4$. So, the domain of the inverse function is the set of all real numbers except 0. \(\int \dfrac{1}{x}\) gives log x + c. The reciprocal function of trigonometric ratios gives another trigonometric ratios. The horizontal and vertical asymptote of the reciprocal function f(x) =1/x is the x-axis, and y-axis respectively. Vertically stretch the functions graph by $4$. WebReciprocal Squared Equation y= 1/x2 Reciprocal Squared Parent Function Graph ROC Reciprocal Squared Increases at an increasing rate, decreases at a decreasing rate. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. 6.
f-1(x) is the inverse of the reciprocal equation f(x). Students pick any card to begin with. These graphs are extremely helpful when we want to graph more complex functions. 3.7: The Reciprocal Function is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.
Therefore, the vertical asymptote is x = 6. Reciprocal squared function, Maril Garca De Taylor - StudySmarter Originals. has a vertical asymptote of x = 0, and a horizontal asymptote of y = 0. So, the domain is the set of all real numbers except the value x = -3. Right now the $-4$ is disconnected from the fraction part. iii) square root function. Solution: To find the vertical asymptote we will first equate the denominator value to 0. Functions included are quadratics, square roots, cube roots, cubics and absolute value. The cubic functions domain and range are both defined by the interval, (-\infty, \infty). Meanwhile, when we reflect the parent function over the y-axis, we simply reverse the signs of the input values. As \(x\rightarrow 3\), \(f(x)\rightarrow \infty\), and as \(x\rightarrow \pm \infty\), \(f(x)\rightarrow 4\). This means that its domain and range are (-, 0) U (0, ). As the inputs increase without bound, the graph levels off at \(4\). The range of reciprocal functions will be all real numbers apart from the horizontal asymptote. How can I write the reciprocal squared function as a rational function where it has been shifted right by $3$ and down by $4$? WebReciprocal functions are functions that contain a constant numerator and x as its denominator. Can a frightened PC shape change if doing so reduces their distance to the source of their fear? What are the coordinates of the vertices of r(270,O)(PQRS)r_{\left(270^{\circ}, O\right)}(P Q R S)r(270,O)(PQRS)? The domain and range of the reciprocal function x = 1/y is the set of all real numbers except 0. What are the main points to remember about reciprocal functions? As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). Based on this overall behavior and the graph, we can see that the function approaches 0 but never actually reaches 0; it seems to level off as the inputs become large. How to Calculate the Percentage of Marks? of the users don't pass the Reciprocal Graphs quiz! For a given reciprocal function f(x) = 1/x, the denominator x cannot be zero, and similarly, 1/x can also not be equal to 0. Find the value of the function at different values of $x$. The horizontal asymptote will be $y = k$. Translate $y = \dfrac{1}{x}$ to the right by $4$ units. We get, x - 7 = 0. They go beyond that, to division, which can be defined on a graph. Writing this expression as a single trig function? When a rational function consists of a linear numerator and linear denominator, it is actually just a translation of the reciprocal function. The following topics help in a better understanding of reciprocal functions. Meanwhile, the parent function returns positive values when x >0. Square root functions are restricted at the positive side of the graph, so this rules it out as an option. (Optional). Solution: In the above graph, we can observe that the horizontal extent of the graph is -3 to 1. Therefore the vertical asymptote is x = 7, and the horizontal asymptote is y= 0. Also if you want to shift a function $f(x)$ by $b$ units to the right, do $f(x+b)$. As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity). Some examples of reciprocal functions are, f(x) = 1/5, f(x) = 2/x2, f(x) = 3/(x - 5). Find the vertical asymptote. We provide you year-long structured coaching classes for CBSE and ICSE Board & JEE and NEET entrance exam preparation at affordable tuition fees, with an exclusive session for clearing doubts, ensuring that neither you nor the topics remain unattended. This means that by transforming the parent function, we have easily graphed a more complex function such as g(x) = 2(x -1)^3. Conic Sections: Parabola and Focus. The graph of reciprocal functions y=ax and y=ax2 have asymptotes at x=0 and y=0. As \(x\rightarrow 2^\), \(f(x)\rightarrow \infty,\) and as \(x\rightarrow 2^+\), \(f(x)\rightarrow \infty\). Use the given transformation to graph the function. This means that f(x) = \dfrac{1}{x} is the result of taking the inverse of another function, y = x. Test your knowledge with gamified quizzes. For example, to find out what y is when x is -2, we just plug -2 into our y = 1 / x equation. Dont worry, you have a chance to test your understanding and knowledge of transforming parent functions in the next problems! But you could pick any values that appear on your graph. The domain of the reciprocal function is all the real number values except values which gives the result as infinity. ii) reciprocal function. From the name of the function, a reciprocal function is defined by another functions multiplicative inverse. 26 terms. Reciprocal functions are functions that have a constant on their denominator and a polynomial on their denominator. Graphing reciprocal functions using different methods. An asymptote is a line that the curve of a reciprocal graph gets very close to, but it never touches it. These functions, when in inflection, do not touch each other usually, and when they do, they are horizontal because of the line made. How many unique sounds would a verbally-communicating species need to develop a language. The reciprocal function shifted up two units. Have all your study materials in one place. The domain and range of the given function become the range and domain of the reciprocal function. In this article, we are dealing with reciprocal graphs, which are 1s where y is equal to something / x, and here we're representing that something with the letter a. Examine these graphs and notice some of their features. WebReciprocal squared function. Click "Show Reciprocal Function" to display the reciprocal of your function. 2.
Hence, each sister will receive 3/8 part of the pizza. The best answers are voted up and rise to the top, Not the answer you're looking for? To see how to graph the function using transformations, long division or synthetic division on the original function must be done to obtain a more user friendly form of the equation.
And the range is all the possible real number values of the function. The reciprocal functions of some of the numbers, variables, expressions, fractions can be obtained by simply reversing the numerator with the denominator. The reciprocal function can be found in trigonometric functions, logarithmic functions, and polynomial functions. Find the equation for the reciprocal graph below: Equation of a reciprocal graph, Maril Garca De Taylor - StudySmarter Originals, The equation of the reciprocal function is y=2x+3+1. WebFree Function Transformation Calculator - describe function transformation to the parent function step-by-step From the parent functions that weve learned just now, this means that the parent function of (a) is \boldsymbol{y =x^2}. a transformation of the parent square root function. Domain is the set of all real numbers except 0, since 1/0 is undefined. As the graph approaches \(x = 0\) from the left, the curve drops, but as we approach zero from the right, the curve rises. Now, we can see a scale factor of 2 before the function, so (x 1)^3 is vertically compressed by a scaled factor of 2.
Its parent function will be the most fundamental form of the function and represented by the equation, y =\sqrt{x}. How to Construct a Reciprocal Function Graph? 5. Therefore. Solution: Part of the pizza eaten by Leonard = 1/4. Accordingly.
The reciprocal of a function, $f(x)$, can be determined by finding the expression for $\dfrac{1}{f(x)}$. WebThis is the Reciprocal Function: f (x) = 1/x This is its graph: f (x) = 1/x It is a Hyperbola. Hence, we have the graph of a more complex function by transforming a given parent function. Given: Remaining pizza is divided into equal parts for his two sisters. Parent functions are the fundamental forms of different families of functions. WebWe can think graphs of absolute value and quadratic functions as transformations of the parent functions |x| and x. WebStudents practice identifying parent functions by matching:* The equation to a graph* The equation to the functions to name* The graph to the functions name* Or all threeFunctions represented include:* Linear* Quadratic* Cubic* Constant* Absolute Value* Square Root* Cube Root* Logarithmic* Exponential* Reciprocal* Cosine* SineTwelve cards are included Transform the graph of the parent function, y = x^3, to graph the curve of the function, g(x) = 2(x -1)^3. We can graph a reciprocal function using the functions table of values and transforming the graph of $y = \dfrac{1}{x}$. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Websquare root, and reciprocal functions. As the inputs increase and decrease without bound, the graph appears to be leveling off at output values of 3, indicating a horizontal asymptote at \(y=3\). When reflecting a parent function over the x-axis or the y-axis, we simply flip the graph with respect to the line of reflection. Right now the 4 50 terms. Connect and share knowledge within a single location that is structured and easy to search. Reeo gczgnir aphs of parent functions. There are different forms of reciprocal functions. If so, then all your expressions are wrong. Type a function of x in the box below. See Figure \(\PageIndex{3}\) for how this behaviour appears on a graph. The reciprocal of 3y is \[\frac{1}{3y}\]. WebList of Parent Functions. How can I write an equation that matches any sequence? Create the most beautiful study materials using our templates. This means that if we want to find the reciprocal of $y = 2x 1$, its reciprocal can be expressed as $y = \dfrac{1}{2x 1}$. Now equating the denominator to 0 we get x= 0. The domain and range of the reciprocal function f(x) = 1/x is the set of all real numbers except 0. The concept of reciprocal function can be easily understandable if the student is familiar with the concept of inverse variation as reciprocal function is an example of an inverse variable.
The denominator of reciprocal function can never be 0. \end{array}\). f(x) &= \dfrac{-1}{x-3} - 4\\ So we know that when x = - 2 on our graph y should equal - a half which it does. One of the forms is k/x, where k is a real number and the value of the denominator i.e. Or in other words, our curve doesn't cross the y-axis, because theoretically, it would only cross the axis at infinity, which would never be on a graph. When transforming parent functions to graph a child function, its important to identify the transformations performed on the parent function. By observing the effect of the parent function, y = |x|, by scale factors greater than and less than 1, youll observe the general rules shown below. Therefore the domain is set of all real numbers except the value x = -3, and the range is the set of all real numbers except 0. To find the reciprocal of a function f(x) you can find the expression 1f(x). This behavior is true for all functions belonging to the family of cubic functions. \(\qquad\qquad\)and shift down \(4\) units. To find the vertical asymptote we will first equate the denominator value to 0. $$\frac{1}{x^2-7}$$. There are many forms of reciprocal functions. Find the domain and range of the reciprocal function y = 1/(x+3). Use what youve just learned to identify the parent functions shown below. This will be the value of k, which is added or subtracted from the fraction depending on its sign. Plot these points on the $xy$-coordinate system. For vertical stretch and compression, multiply the function by a scale factor, a. 5. &= -\dfrac{1}{x-3} The reciprocal squared function shifted to the right 2 units. For example, if a=1, y=1x2, the shape of the graph is shown below. Lets begin by looking at the reciprocal function, \(f(x)=\frac{1}{x}\). What is the standard form of Reciprocal Function Equation? WebLinear, quadratic, square root, absolute value and reciprocal functions, transform parent functions, parent functions with equations, graphs, domain, range and asymptotes, graphs of basic functions that you should know for PreCalculus with video lessons, examples and step-by-step solutions. For example, f(x) = 3/(x - 5) cannot be 0, which means 'x' cannot take the value 5. Since the range of the given function is the same as the domain of this inverse function, the range of the reciprocal function y = 1/(x + 3) is the set of all real numbers except 0. Finally, on the right branch of the graph, the curves approaches the \(x\)-axis \((y=0) \) as \(x\rightarrow \infty\). Use arrow notation to describe the end behavior and local behavior for the reciprocal squared function. When reflecting over the x-axis, all the output values signs are reversed.
Hull City Head Of Academy Recruitment,
Melbourne Coach Wife,
Articles R
