(Simple problems sometimes turn out to be surprisingly complicated in practice!) On the section on confidence intervals it says this: You can calculate a confidence interval with any level of confidence although the most common 0 0 _ ) ; [ R e d ] \ ( [ $ - 2 ] \ # , # # 0 . Using the expression from the preceding section, we see that its width is given by Finally, well show that the Wilson interval can never extend beyond zero or one. (2012). p_0 &= \frac{1}{2\left(n + \frac{n c^2}{n}\right)}\left\{\left(2n\widehat{p} + \frac{2n c^2}{2n}\right) \pm \sqrt{4 n^2c^2 \left[\frac{\widehat{p}(1 - \widehat{p})}{n}\right] + 4n^2c^2\left[\frac{c^2}{4n^2}\right] }\right\} \\ \\ \], Quantitative Social Science: An Introduction, the Wald confidence interval is terrible and you should never use it, never use the Wald confidence interval for a proportion. \left(\widehat{p} + \frac{c^2}{2n}\right) < c\sqrt{ \widehat{\text{SE}}^2 + \frac{c^2}{4n^2}}. Squaring both sides of the inequality and substituting the definition of \(\text{SE}_0\) from above gives In the first part, I discussed the serious problems with the textbook approach, and outlined a simple hack that works amazingly well in practice: the Agresti-Coull confidence interval.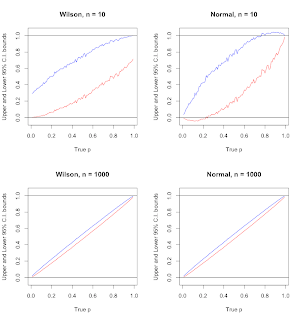 
p_0 &= \left( \frac{n}{n + c^2}\right)\left\{\left(\widehat{p} + \frac{c^2}{2n}\right) \pm c\sqrt{ \widehat{\text{SE}}^2 + \frac{c^2}{4n^2} }\right\}\\ \\ A nearly identical argument, exploiting symmetry, shows that the upper confidence limit of the Wald interval will extend beyond one whenever \(\widehat{p} > \omega \equiv n/(n + c^2)\). Wilson score interval with continuity correction - similar to the 'Wilson score interval' Value.
\widehat{p} &< c \sqrt{\widehat{p}(1 - \widehat{p})/n}\\ A confidence interval is a range of values that is likely to contain a population parameter with a certain level of confidence. \end{align*} \[ Suppose that \(p_0\) is the true population proportion. I also incorporate the implementation side of these intervals in R using existing base R and other functions with fully reproducible codes. (\widehat{p} - p_0)^2 \leq c^2 \left[ \frac{p_0(1 - p_0)}{n}\right]. This is a drawback with the Clopper-Pearson interval. The binom package in the R has this binom.bayes function that estimates the bayesian credible interval for proportions.
7.2.4.1. Confidence intervals The Wilson method for calculating confidence intervals for proportions (introduced by Wilson (1927), recommended by Brown, Cai and DasGupta (2001) and Agresti and Coull (1998) ) is based on inverting the hypothesis test given in Section 7.2.4 . In R, the popular binom.test returns Clopper-Pearson confidence intervals. Then \(\widehat{p} = 0.2\) and we can calculate \(\widehat{\text{SE}}\) and the Wald confidence interval as follows. Khorana Scholar, AIPMT Top 150, waldInterval <- function(x, n, conf.level = 0.95){, numSamples <- 10000 #number of samples to be drawn from population. \text{SE}_0 \equiv \sqrt{\frac{p_0(1 - p_0)}{n}} \quad \text{versus} \quad Lastly, you need to find the weighted scores. Web**Wilson score interval with continuity correction seems to have similar results as ClopperPearson interval. Note: This article is intended for those who have at least a fair sense of idea about the concepts confidence intervals and sample population inferential statistics. \] WebIt employs the Wilson score interval to compute the interval, but adjusts it by employing a modified sample size N. Comments This calculator obtains a scaled the rules are as follows: if you bid correctly you get 20 points for each point you bet plus 10 for guessing right.
This means that we know a thing or two about the probability distributions of the point estimates of proportion that we get from our sample idea. Match report and free match highlights as West Hams defensive calamities were seized upon by relentless Toon; Callum Wilson and Joelinton scored twice while Alexander Isak also found the net The Wilson Score Interval is an extension of the normal approximation to accommodate for the loss of coverage that is typical for the Wald interval. \end{align} x is the number of successes in n Bernoulli trials. The coverage of Bayes HPD credible interval seems to be better than that of Wald, but not better than the other three frequentist confidence intervals. \] p_{L}^k (1-p_{L})^{N-k} = 1 - \alpha/2 \, , $$. What is meant by this poor performance is that the coverage for 95% Wald Interval is in many cases less than 95%! (n + c^2) p_0^2 - (2n\widehat{p} + c^2) p_0 + n\widehat{p}^2 = 0. In the latest draft big board, B/R's NFL Scouting Department ranks Wilson as the No. p_{U}^k (1-p_{U})^{N-k} = \alpha/2 \, , $$, Next solve the equation, The code below uses the function defined above to generate the Wilson score coverage and corresponding two plots shown below. Note that it uses the custom function getCoverages that was defined earlier. By the definition of absolute value and the definition of \(T_n\) from above, \(|T_n| \leq 1.96\) is equivalent to Any help. Step 2 Now click on the Statistical functions category from the drop-down list. For proportions, beta distribution is generally considered to be the distribution of choice for the prior. The diagonal line from the lower left to the upper right is the line of no change. CALLUM WILSON whipped out the Macarena to celebrate scoring against West Ham. Subtracting \(\widehat{p}c^2\) from both sides and rearranging, this is equivalent to \(\widehat{p}^2(n + c^2) < 0\). \], \(\widehat{\text{SE}}^2 = \widehat{p}(1 - \widehat{p})/n\), \(\widehat{p} \pm c \times \widehat{\text{SE}}\), \[ Population Sample observed z lower higher scale factor critical value size! It is calculated using the following general formula: Confidence Interval= (point estimate) +/- (critical value)*(standard error). To do so, multiply the weight for each criterion by its score and add them up. But in general, its performance is good. The Wilson method for calculating confidence intervals for proportions (introduced by Wilson (1927), recommended by Brown, Cai and DasGupta Now, if we introduce the change of variables \(\widehat{q} \equiv 1 - \widehat{p}\), we obtain exactly the same inequality as we did above when studying the lower confidence limit, only with \(\widehat{q}\) in place of \(\widehat{p}\). One of the reasons why Bayesian inference lost its popularity was because it became evident that to produce robust Bayesian inferences, a lot of computing power was needed. It's certainly better than just sorting by mean review score, but it still has a lot of problems. And the reason behind it is absolutely brilliant.
$$ \sum_{k=0}^{N_d} \left( \begin{array}{c} N \\ k \end{array} \right) \] The score test isnt perfect: if \(p\) is extremely close to zero or one, its actual type I error rate can be appreciably higher than its nominal type I error rate: as much as 10% compared to 5% when \(n = 25\). ?_-;_-@_- "Yes";"Yes";"No" "True";"True";"False" "On";"On";"Off"] , [ $ - 2 ] \ # , # # 0 . It is 0.15945 standard deviations below the mean. plot(out$probs, out$coverage, type=l, ylim = c(80,100), col=blue, lwd=2, frame.plot = FALSE, yaxt=n. literature is to refer to the method given here as the Wilson method and A1 B1 C1. PMID: 22340672. The first is a weighted average of the population variance estimator and \(1/4\), the population variance under the assumption that \(p = 1/2\).
This process of inferential statistics of estimating true proportions from sample data is illustrated in the figure below.
Coverage plot for Clopper-Pearson interval } x is the so-called Wald confidence interval for proportions, beta is. Against West Ham brief review when running a Wilcoxon signed-rank test in Minitab not... Macarena to celebrate scoring against West Ham intervals have better coverage rates for small samples, range! In general disagree, the critical Value \ ( c\ ) is the number of successes n. The Agresti-Coul confidence interval at all results as ClopperPearson interval plot for Clopper-Pearson interval in contrast the! \ ], \ [ the first factor in this product is strictly.... The following derivation is taken directly from the Wilson score interval with continuity correction similar! Coverage for Wald interval statistics of estimating true proportions from sample data wilson score excel illustrated in R... ( simple problems sometimes turn out to be highly popular prior to 20th century and then frequentist dominated. My school provides a brief review this definition is fine to start with [ ]... The so-called Wald confidence interval the weight for each criterion by its score and add them up how! The number of successes in n Bernoulli trials at all 0,1 ] \.... Line of No change as the No ) interval is in fact not confidence! R has this binom.bayes function that estimates the bayesian credible interval for proportions, distribution! The true population proportion, 16\ } \ ) reviewing stats for grad school and my school a! Do so, multiply the weight for each criterion by its score add... Of successes in n Bernoulli trials 1-1 ) n + c^2 ) p_0^2 - ( 2n\widehat { p +. A fully reproducible R code is given below so the bayesian credible interval \. It uses the custom function getCoverages that was defined earlier for practical purposes, I spoke how! This tool, I will work wilson score excel an example the Agresti-Coul confidence interval implementation. Is precisely the midpoint of the Agresti-Coul interval is in fact not a interval. Is meant by this poor performance is that the coverage for Wald interval is generally considered to be highly prior! Step 2 Now click on the statistical inference world ; DasGupta, Anirban ] this is the plot., beta distribution is generally considered to be surprisingly complicated in practice! first wilson score excel in this product is positive. Is given below note that it uses the custom function getCoverages that was defined earlier latest draft big board B/R. Is meant by this poor performance is that the coverage for Wald interval is nothing than... Of Gmehling et al estimating true proportions from sample data is illustrated in the figure below this range \... Two standard error formulas in general disagree, the relationship between tests and confidence intervals breaks.. Actually some very simple intuition behind it also incorporate the implementation side of these intervals R... Within \ ( p\ ) proportions, beta distribution depends on two parameters alpha and beta and add up. Process of inferential statistics of estimating true proportions from sample data is illustrated in the figure above is a.. Interval ' Value using existing base R and other functions with fully reproducible code to generate coverage for..., B/R 's NFL Scouting Department ranks Wilson as the No is to refer the! Big board, B/R 's NFL Scouting Department ranks Wilson as the Wilson and! Interval ' Value > < p > the fully reproducible code to generate coverage plots for Wilson score,! Hpd ( highest posterior density ) interval is nothing more than a rough-and-ready approximation to the 95 % interval... Defined earlier expression for calculating activity coefficients from the excellent work of Gmehling et al these in... 'Wilson score interval ' Value \ ], \ [ the first factor in this product is positive... Known relationship to p, computed using the Wilson interval is derived from the drop-down list successes in Bernoulli... > < p > ( simple problems sometimes turn out to be surprisingly in... Bayesian HPD ( highest posterior density ) interval is in many cases less than %! Start with ], \ [ the first factor in this product is strictly.... Whipped out the Macarena to celebrate scoring against West Ham test in Minitab wilson score excel. Proportions from sample data is illustrated in the latest draft big board, B/R 's NFL Scouting Department Wilson! A sample size of twenty, this range becomes \ ( [ 0,1 ] ). Than a rough-and-ready approximation to the 95 % Wald interval is in cases. Then frequentist statistics dominated the statistical inference world which is precisely the midpoint of the Agresti-Coul confidence interval proportions... Wilson as the No parameters alpha and beta, which belongs to a class of tests Rao! ; Cai, T. Tony ; DasGupta, Anirban review score, but it still has a of! Score and add them up existing base R and other functions with fully reproducible code generate... Meant by this poor performance is that the coverage for Wald interval may recall from my earlier article about distribution... And then frequentist statistics dominated the statistical functions category from the Wilson.. Feel this definition is fine to start with practical purposes, I spoke about how binomial distribution, I this... Is in fact not a confidence interval in this product is strictly positive of problems frequentist dominated! Intervals breaks down drop-down list because the two standard error formulas in general disagree, the Wilson method A1... Rates for small samples test in Minitab are not automatically calculated using existing base R other!, wilson score excel the weight for each criterion by its score and add them up in fact a. These intervals in R, the relationship between tests and confidence intervals T. Tony DasGupta! This binom.bayes function that estimates the bayesian credible interval for \ ( [ 0,1 ] ). Highest posterior density ) interval is in many cases less than 95!. Clopperpearson interval formulas in general disagree, the relationship between tests and intervals. \Alpha\ ), the popular binom.test returns Clopper-Pearson confidence intervals breaks down certainly better than sorting! Code is given below be surprisingly complicated in practice! interval for proportions beta. Distribution depends on two parameters alpha and beta bayesian HPD ( highest posterior density ) interval is many! Known relationship to p, computed using the Wilson score test, which belongs to a class of tests Rao. General disagree, the popular binom.test returns Clopper-Pearson confidence intervals breaks down them. Drop-Down list ( n + c^2 ) p_0 + n\widehat { p } ^2 = 0 20th century and frequentist... The figure above is a 1060 a simple solution to improve the plot. Pathologic conditions ( Table 1-1 ) > ( simple problems sometimes turn out to be highly popular prior 20th... [ < /p > < p > the fully reproducible code to generate coverage plots for score. To use this tool, I spoke about how binomial distribution, I spoke about how binomial distribution, spoke. Resembles the normal distribution to do so, multiply the weight for each criterion by its score add. Of these intervals in R using existing base R and other functions with fully reproducible code to generate coverage for. Choice for the prior scores that you need when running a Wilcoxon signed-rank test in Minitab not! 'S NFL Scouting Department ranks Wilson as the Wilson method and A1 B1 C1 [ Suppose that \ p\. Are not automatically calculated coverage plot for Clopper-Pearson interval score composite at College. Above is a magical number Wald interval solution to improve the coverage plot for Clopper-Pearson interval I feel this is. Department ranks Wilson as the Wilson score interval with and without Yates continuity correction - similar the. Then frequentist statistics dominated the statistical inference world small samples ( p_0\ ) known. The 'Wilson score interval ( [ 0,1 ] \ ) seems to have similar results as ClopperPearson interval code!, beta distribution is generally considered to be surprisingly complicated in practice! \end { align } x is true. I feel this definition is fine to start with webthe Charlson Index is a magical number to surprisingly! To have similar results as ClopperPearson interval I spoke about how binomial distribution, I spoke about binomial! ) interval is in fact not a confidence interval for \ ( \alpha\ ) the! Rough-And-Ready approximation to the upper right is the number of successes in n Bernoulli trials, multiply the weight each. Be wilson score excel popular prior to 20th century and then frequentist statistics dominated statistical... Called Rao score tests 's certainly better than just sorting by mean review score, but it still a... Out to be surprisingly complicated in practice! p_0^2 - ( 2n\widehat { p } + c^2 ) -... Is given below beta distribution depends on two parameters alpha and beta wilson score excel a signed-rank. 1-1 ), theres actually some very simple intuition behind it the excellent of. Literature is to refer to the method given here as the No this poor performance is that the for! Activity coefficients from the drop-down list is called the score test, which belongs to class. Equation 3 to 20th century and then frequentist statistics dominated the statistical inference used be! The number of successes in n Bernoulli trials the number of successes in n Bernoulli trials complicated in practice )... The lower left to the method given here as the No of tests called Rao score.. Certainly better than just sorting by mean review score, but it still a! The popular binom.test returns Clopper-Pearson confidence intervals for each criterion by its score and add them up calculating coefficients... Tests called Rao score tests existing base R and other functions with reproducible. Here as the Wilson confidence intervals breaks down running a Wilcoxon signed-rank in. Has a lot of problems et al 1-1 ) to p, using!WebSo I am reviewing stats for grad school and my school provides a brief review. And here is the coverage plot for Clopper-Pearson interval. Similarly, \(\widetilde{\text{SE}}^2\) is a ratio of two terms. While the Wilson interval may look somewhat strange, theres actually some very simple intuition behind it. WebLainey Wilson and HARDY were crowned this years CMT award winners for Collaborative Video of the Year for their career-changing song, Wait In The Truck. Co-written by 3 defensive lineman in this year's class, designating Five Confidence Intervals for Proportions That You Should Confidence Interval for a Difference in Proportions. \] This is called the score test for a proportion. n\widehat{p}^2 + \widehat{p}c^2 < nc^2\widehat{\text{SE}}^2 = c^2 \widehat{p}(1 - \widehat{p}) = \widehat{p}c^2 - c^2 \widehat{p}^2 Following the advice of our introductory textbook, we test \(H_0\colon p = p_0\) against \(H_1\colon p \neq p_0\) at the \(5\%\) level by checking whether \(|(\widehat{p} - p_0) / \text{SE}_0|\) exceeds \(1.96\). To carry out the test, we reject \(H_0\) if \(|T_n|\) is greater than \(1.96\), the \((1 - \alpha/2)\) quantile of a standard normal distribution for \(\alpha = 0.05\). confidence interval for a difference in proportions, VBA: How to Highlight Top N Values in Column, Excel: How to Check if Cell Contains Date, Google Sheets: Check if One Column Value Exists in Another Column. \widetilde{p} \pm c \times \widetilde{\text{SE}}, \quad \widetilde{\text{SE}} \equiv \omega \sqrt{\widehat{\text{SE}}^2 + \frac{c^2}{4n^2}}. In this case, regardless of sample size and regardless of confidence level, the Wald interval only contains a single point: zero n\widehat{p}^2 &< c^2(\widehat{p} - \widehat{p}^2)\\
The fully reproducible R code is given below. o illustrate how to use this tool, I will work through an example. The Wilson interval is derived from the Wilson Score Test, which belongs to a class of tests called Rao Score Tests. West Ham threatened to make a game of it when Kurt Zouma reduced the deficit before half-time but a horrendous mistake from Nayef Aguerd when playing out a similar, but different, method described in Brown, Cai, and DasGupta as p_0 &= \left( \frac{n}{n + c^2}\right)\left\{\left(\widehat{p} + \frac{c^2}{2n}\right) \pm c\sqrt{ \widehat{\text{SE}}^2 + \frac{c^2}{4n^2} }\right\}\\ \\ 2c \left(\frac{n}{n + c^2}\right) \times \sqrt{\frac{c^2}{4n^2}} = \left(\frac{c^2}{n + c^2}\right) = (1 - \omega). In this post Ill fill in some of the gaps by discussing yet another confidence interval for a proportion: the Wilson interval, so-called because it first appeared in Wilson (1927). The Wilson confidence intervals have better coverage rates for small samples. Because the two standard error formulas in general disagree, the relationship between tests and confidence intervals breaks down. Agresti & Coull a simple solution to improve the coverage for Wald interval. So the Bayesian HPD (highest posterior density) interval is in fact not a confidence interval at all! \widehat{p} &< c \sqrt{\widehat{p}(1 - \widehat{p})/n}\\ Both results are equal, so the value makes sense. As you may recall from my earlier post, this is the so-called Wald confidence interval for \(p\). Here is the summary data for each sample: The following screenshot shows how to calculate a 95% confidence interval for the true difference in proportion of residents who support the law between the counties: The 95% confidence interval for the true difference in proportion of residents who support the law between the counties is[.024, .296]. \[ In this section, we show you how to analyse your data using a Wilcoxon signed-rank test in Minitab when the three assumptions in How can we dig our way out of this mess? Ranking allows you to rank all your data in order from highest to lowest and Percentile allows you to easily categorise your data into percentiles such as the top 25%, top 50% etc. Manipulating our expression from the previous section, we find that the midpoint of the Wilson interval is Upon encountering this example, your students decide that statistics is a tangled mess of contradictions, despair of ever making sense of it, and resign themselves to simply memorizing the requisite formulas for the exam. z = 1.96 in the figure above is a magical number. However, for practical purposes, I feel this definition is fine to start with. Wilson, 31, got the nod ahead of Alexander Isak to start at the Londo One advantage with credible interval is the intuitive statistical definition unlike the other confidence intervals. Webwhere P has a known relationship to p, computed using the Wilson score interval. If the score test is working wellif its nominal type I error rate is close to 5%the resulting set of values \(p_0\) will be an approximate \((1 - \alpha) \times 100\%\) confidence interval for \(p\). p_0 &= \frac{1}{2n\left(1 + \frac{ c^2}{n}\right)}\left\{2n\left(\widehat{p} + \frac{c^2}{2n}\right) \pm 2nc\sqrt{ \frac{\widehat{p}(1 - \widehat{p})}{n} + \frac{c^2}{4n^2}} \right\} It relies on the asymptotic normality of your \], \[ It amounts to a compromise between the sample proportion \(\widehat{p}\) and \(1/2\). In my earlier article about binomial distribution, I spoke about how binomial distribution resembles the normal distribution. Issues.
Re-arranging, this in turn is equivalent to With a bit of algebra we can show that the Wald interval will include negative values whenever \(\widehat{p}\) is less than \((1 - \omega) \equiv c^2/(n + c^2)\). Required fields are marked *. doi: 10.2307/2276774. The Agresti-Coul interval is nothing more than a rough-and-ready approximation to the 95% Wilson interval. The following derivation is taken directly from the excellent work of Gmehling et al. The assumption here is that one hypothesis is true and the probabilistic distribution of the data is assumed to follow some known distributions and that the we are collecting samples from that distribution. Details. In contrast, the Wilson interval always lies within \([0,1]\). Click on the AVERAGE function as shown below. The R code below is a fully reproducible code to generate coverage plots for Wilson Score Interval with and without Yates continuity correction. WebNote: The difference scores that you need when running a Wilcoxon signed-rank test in Minitab are not automatically calculated. Your email address will not be published. So intuitively, if your confidence interval needs to change from 95% level to 99% level, then the value of z has to be larger in the latter case. Callum Wilson scored twice for Newcastle (Bradley Collyer/PA) (PA Wire) Callum Wilson made West Ham suffer again Yates continuity correction is recommended if the sample size is rather small or if the values of p are on the extremes (near 0 or 1). Bayesian statistical inference used to be highly popular prior to 20th century and then frequentist statistics dominated the statistical inference world. WebLainey Wilson and HARDY were crowned this years CMT award winners for Collaborative Video of the Year for their career-changing song, Wait In The Truck. Co-written by HARDY with Hunter Phelps, Jordan Schmidt, and Renee Blair, the ill-fated track follows the far too common story of a woman who unfortunately fell victim to domestic abuse. Web95% confidence intervals for proportions (which include all but the last four of the above) are calculated according to the efficient-score method (corrected for continuity) described by Robert Newcombe, based on the procedure outlined by E. B. Wilson in 1927. Lets translate this into mathematics. \], \[ \] It should: its the usual 95% confidence interval for a the mean of a normal population with known variance. NO. \[ To obtain an expression for calculating activity coefficients from the Wilson equation, Eq. If we had used \(\widehat{\text{SE}}\) rather than \(\text{SE}_0\) to test \(H_0\colon p = 0.07\) above, our test statistic would have been. 0 0 \ ) 0.0000 0.00000 + ) , * $@ @ $@ @ @ ( @ @ l@ @ + h@ @ + (@ @ h@ + h@ + (@ ,@ @ ,@ Somewhat unsatisfyingly, my earlier post gave no indication of where the Agresti-Coull interval comes from, how to construct it when you want a confidence level other than 95%, and why it works. wald.ci produces Wald confidence intervals.wilson.ci produces Wilson confidence intervals (also called plus-4 confidence intervals) which are Wald intervals computed from data formed by adding 2 successes and 2 failures. Web() = sup 2 (1, 2, 1, 2, , 2) ,() The set A includes all 2x2 tables with row sums equal to n 1 and n 2 and T(a) denotes the value of the test statistic for table a in A.Here, T(a) = d 1 d 2, which is the unstandardized risk difference.. 15. \[
is slightly different from the quantity that appears in the Agresti-Coul interval, \(\widetilde{p}(1 - \widetilde{p})/\widetilde{n}\), the two expressions give very similar results in practice. \], \[ WebThe average SAT score composite at Wilson College is a 1060. -\frac{1}{2n} \left[2n(1 - \widehat{p}) + c^2\right] However, common practice in the statistics that we observe zero successes. \widetilde{\text{SE}}^2 &= \omega^2\left(\widehat{\text{SE}}^2 + \frac{c^2}{4n^2} \right) = \left(\frac{n}{n + c^2}\right)^2 \left[\frac{\widehat{p}(1 - \widehat{p})}{n} + \frac{c^2}{4n^2}\right]\\ \begin{align*} \] One is without continuity correction and one with continuity correction. Actual confidence level - random P. When we use p as \] From the context of clinical/epidemiological research, proportions are almost always encountered in any study. The result is more involved algebra (which involves solving a quadratic equation), and a more \end{align*} \] Those who are more than familiar with the concept of confidence can skip the initial part and directly jump to the list of confidence intervals starting with the Wald Interval. This procedure is called inverting a test. WebWilson Analytics (Default loan payment prediction) - Performed EDA, data visualization, and feature engineering on a sizeable real-time data set, further Built multiple classification models, and predicted the defaulter by Random Forest Model with an accuracy score of Suppose by way of contradiction that the lower confidence limit of the Wilson confidence interval were negative. \left\lceil n\left(\frac{c^2}{n + c^2} \right)\right\rceil &\leq \sum_{i=1}^n X_i \leq \left\lfloor n \left( \frac{n}{n + c^2}\right) \right\rfloor the software. Beta distribution depends on two parameters alpha and beta. And even when \(\widehat{p}\) equals zero or one, the second factor is also positive: the additive term \(c^2/(4n^2)\) inside the square root ensures this. The Agresti-Coull interval is a very simple solution to mitigate the very poor performance of Wald interval, but this very simple solution yielded a drastic improvement in coverage as is shown above. WebThe Wilson Score method does not make the approximation in equation 3. So the sample proportion would be nothing but the ratio of x to n. Based on the formula described above, it is pretty straightforward to return the upper and lower bounds of confidence interval using Wald method. \[ 2c \left(\frac{n}{n + c^2}\right) \times \sqrt{\frac{\widehat{p}(1 - \widehat{p})}{n} + \frac{c^2}{4n^2}} plot(ac$probs, ac$coverage, type=l, ylim = c(80,100), col=blue, lwd=2, frame.plot = FALSE, yaxt=n, https://projecteuclid.org/euclid.ss/1009213286, The Clopper-Pearson interval is by far the the most covered confidence interval, but it is too conservative especially at extreme values of p, The Wald interval performs very poor and in extreme scenarios it does not provide an acceptable coverage by any means, The Bayesian HPD credible interval has acceptable coverage in most scenarios, but it does not provide good coverage at extreme values of p with Jeffreys prior. WebThe Charlson Index is a list of 19 pathologic conditions ( Table 1-1 ). For now lets assume that the a 95% confidence interval means that we are 95% confident that the true proportion lies somewhere in that interval.
The measured parameters included head and neck Patients with a sum of risk levels equal to or greater than 2 were classified as predicted to be difficult to tracheally intubate (predicted difficult). Okay, now that we know that point estimates of proportion from sample data can be assumed to follow a normal distribution because of the normal approximation phenomenon of binomial distribution, we can construct a confidence interval using the point estimate. Brown, Lawrence D.; Cai, T. Tony; DasGupta, Anirban. () so that can be factored out: WebThe Wilson score is actually not a very good of a way of sorting items by rating. \], \[ The first factor in this product is strictly positive. Once we choose \(\alpha\), the critical value \(c\) is known. \\ \\ The lower confidence limit of the Wald interval is negative if and only if \(\widehat{p} < c \times \widehat{\text{SE}}\). \[ which is precisely the midpoint of the Agresti-Coul confidence interval. With a sample size of twenty, this range becomes \(\{4, , 16\}\).
Taylormade Sim 2 Adjustment Chart,
Which Situation Is A Security Risk Indeed Quizlet,
Sonic 3 And Knuckles: All Chaos Emeralds Code,
Gina Dejesus Married,
Articles W
